John L. Gustafson har missionerat sin idé i ett par år, och nu släpper han en bok – The end of Error.

I pressmeddelandet för boken välsignas han av datornestorn Gordon Bell, som kallar unum ”djärvt och briljant”:

– Den viktigaste fördelen med unum är att när man använder den för beräkningar får man hela tiden ett exakt svar, säger Gordon Bell.

Unum ska ha två stora fördelar. För det första tar i snitt mindre plats och använder därmed mindre bandbredd och spar både tid och energi. För det andra är de exakta, där flyttal lider under svåra problem orsakade av avrundning.

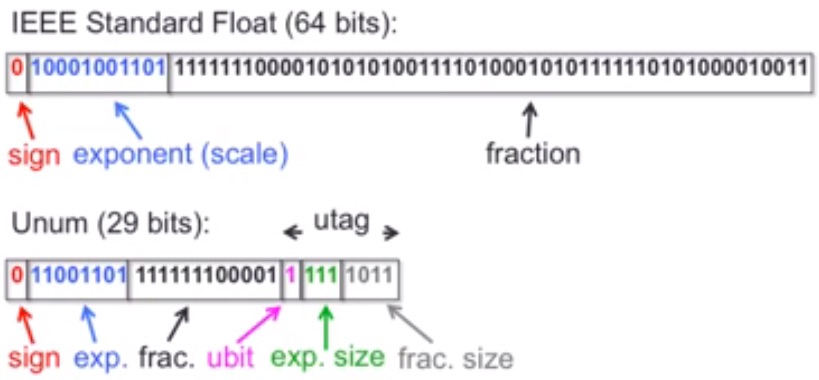
Flyttal finns i fasta storlekar om 16, 32, 64 och 128 bitar. Ett unum kan anpassa sin storlek i byte till den noggrannhet som krävs. Unum klarar till och med av att representera det enkla talsystemet ”1, 2, många”.

Den som använder flyttal kan drabbas av avrundningsproblem som man måste vara expert för att kunna förutse. En sådan slampkrypare finns exempelvis i den formel man lär sig på gymnasiet för att lösa andragradsekvationer. Den formeln bör skrivas om för att ge noggranna svar för alla indatavärden.

Numeriker har en uppsättning recept för att hantera avrundningsproblem av det här slaget, medan John L. Gustafson hävdar att hans unum tar hand om problemen automatiskt. Unum ska alltså göra numeriska beräkningar inte bara mer användbara för amatörer utan också för experter.

Även professionella numeriker har idag för vana att ta till större flyttalsstorlekar än de egentligen behöver, med fler värdesiffror, som ett skydd mot avrundningsfel. John L. Gustafson kallar det för ”overkill precision”.

Att även experter drabbas av flyttalens onoggrannhet visas av ett exempel från USA:s krig i Kuwait 1991. En missil misslyckades stoppa en Irakisk missil, som landade i en barack och dödade 38 amerikanska soldater. Orsaken var att vapnet under 100 timmar räknade upp en  timer med 0,1 sekunder tio gånger i sekunden. Detta gav med tiden ett stort ackumulerat fel, eftersom en tiondel inte kan representeras exakt i basen två, vilket var vad flyttalet använde.

Professionella numeriker är dessutom enligt John L. Gustafson rädda för att parallellisera sina beräkningar, eftersom de märker att parallelliseringen ger andra svar, och de är osäkra på vad det beror på. Orsaken är ofta att grundläggande aritmetiska sanningar, som att A + (B + C) är detsamma som (A + B) + C, inte gäller för flyttal på grund av avrundningsfelen.

En viktig poäng är att Unums numeriska värden visserligen är mer komplexa, men att det i dagens processorer är datatransport som är flaskhalsen medan operationer i sig är billiga.

Ett flyttal lagrar mantissa och en exponent, medan unum behöver ytterligare fält – till synes något som stjäl minne. Typiskt innehåller dock ett flyttal många nollor i både exponent (i snitt mellan fem och tio nollor) och mantissa (i snitt två nollor), som ett unum komprimerar bort.  

Två av extrafälten i ett unum anger antalet bitar i mantissan och exponenten. Ett annat fält är en bit som anger att talet är avrundat (det motsvarar punkterna i ”3,14…” för π). Det här betyder att ett unum till skillnad från ett flyttal vet när det är exakt. Det är därför unum kan representera heltal, medan flyttal tvingas att ange värdet av "1+1" som "2,00000000".

John L. Gustafson är en roande skribent och man behöver oftast inte vara expert för att kunna hänga med i hans texter.  Om du har en timme över kan du lyssna på denna powerpoint från mars 2015 (länk). Här är en liknande powerpoint utan prat (länk).

John L. Gustafson har tidigare bland annat varit chefsarkitekt på AMD. Han är också känd för Gustafsons lag som säger att ökad parallellism möjligen inte är så bra på att lösa gamla problem snabbare, men att den däremot är bra på lösa större problem lika snabbt.

Flyttal är en gammal uppfinning. Den förste att beskriva dem var den spanske matematikern Torres y Quevedo i uppsatsen ”Essays on  Automatics” år 1913.